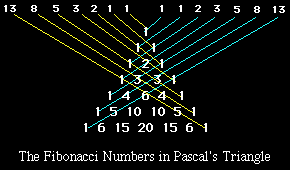~ piscean ♓ delusions - pisces art, photo, video, image, web and digital arts

Interpretations - Sacred Knowledge - The Fibonacci Sequence

piscean delusions - pisces art, all about pisces, information and more.

The Fibonacci sequence (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 . . .) occurs throughout the worlds of nature, art, music, and mathematics!

Each term in the series is produced by adding together the two previous terms, so that 1 + 1=2, 1 + 2=3, 2 + 3=5, and so on. The sequence takes its name from a famous thirteenth-century European mathematician, Leonard of Pisa (?1170-1250), also called Fibonacci.

fibbonacci

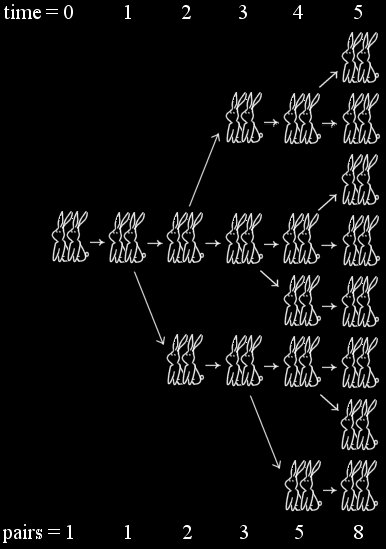
Fibonacci was one of the first Europeans to use Arabic numbers, whose use he explained in his 1202 Liber abaci.Fibonacci gave this sequence as an answer to the following mathematical puzzle:

A certain man put a pair of rabbits in a place surrounded on all sides by a wall. How many pairs of rabbits can be produced from that pair in a year if it is supposed that every month each pair begets a new pair which from the second month on becomes productive?

The answer is the sequence 1, 1, 2, 3, 5, 8, 13, 21, . ., as illustrated below:

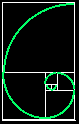
Fibonacci numbers occur many times in the natural world. Plants tend to have a number of leaves that is a Fibonacci number, and flowers have a Fibonacci number of petals. Seeds in a flower head are often arranged in spiral patterns that are related to Fibonacci numbers (for example, the number of spirals that curve to the left and the number of spirals that curve to the right will be adjacent numbers in the Fibonacci sequence).Spiral shells also exhibit patterns related to the Fibonacci sequence:

* It should be noted that, according to a Science News article entitled "Sea Shell Spirals" says that Nautilus Shells actually have a ratio that differs from the ratio of the Golden Spiral. The article notes that in 1999, retired mathematician Clement Falbo measured a series of nautilus shells at San Francisco's California Academy of Sciences, and he found that while they were indeed logarithmic spirals (like the golden spiral), their ratios ranged from about 1.24 to 1.43, with an average ratio of about 1.33 to 1, not even close to the 1.618... ratio of the Golden Spiral.

Fibonacci numbers are also important in art and music. The ratio between successive Fibonacci numbers approximates an important constant called "the golden mean" or sometimes phi, which is approximately 1.61803. The higher you go in the Fibonacci sequence, the more closely the ratio between two successive numbers in the sequence approximates phi. (By the way phi2=phi + 1!)
A rectangle whose sides are in the proportion 1 : 1.61803 is supposed to be the most aesthetically perfect rectangle (the "golden rectangle"). The Parthenon in Athens has such a rectangle as its face, and phi is said to have figured in the construction of the Great Pyramids. The "golden section," in which a line is divided into segments of lengths in the ratio 1 : .61803 is supposed to be an aesthetically ideal way to divide a line.

Numerous artists have used the golden section in their works, as well as composers, including (perhaps) Beethoven and Mozart.By the way, the Fibonacci sequence also shows up in Pascal's triangle, if you add the diagonals!